Μια άσκηση - διδασκαλία στην ορμή και στην Α.Δ.Ο.
Μια άσκηση ...Ένα μάθημα στα κύματα.
Μια διασκευή...(Δογραματζακης)
Μια στρεφόμενη εικόνα . Ο γύρος του Θανάτου.
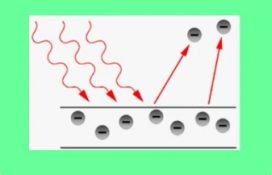
Στοιχεία Κβαντικής Θεωρίας Ερωτήσεις (1)
Τα ρευστά...με τα μάτια του Φυσικού. Μέρος Α . Σωματίδιο του Ρευστού (1)
Το δάκρυ της Μαρίας ...και μια ιδιόμορφη περιοδική κίνηση.
Τρεις ιδέες ...για μια τροχαλία. (1)
H AΔΟ ...Ο 3ος Ν.ΝΕΥΤΩΝΑ ΚΑΙ ΟΙ Χ.Α.
OKTΩ ΠΡΟΤΑΣΕΙΣ ΣΤΙΣ ΜΗΧ.ΤΑΛΑΝΤΩΣΕΙΣ
Γιατί ΣF=- Dx και όχι ΣF= Dx _
Γιατί ‘γραμμική αρμονική ταλάντωση’ και όχι … ‘ευθύγραμμη αρμονική ταλάντωση’_
Ένα επαναληπτικό μάθημα στην Ά Λυκείου.
Η Μπλε πανσέληνος του αποχεραιτισμού(2) (1)